Create accountLogin

Recent searches

No recent searches

Search options

Only available when logged in.
mastodon.gamedev.place is one of the many independent Mastodon servers you can use to participate in the fediverse.
Mastodon server focused on game development and related topics.

Administered by:

Server stats:

5.1K
active users

mastodon.gamedev.place: AboutProfiles directoryPrivacy policy

Mastodon: AboutGet the appKeyboard shortcutsView source codev4.3.7

Quiet public
Rune Skovbo Johansen

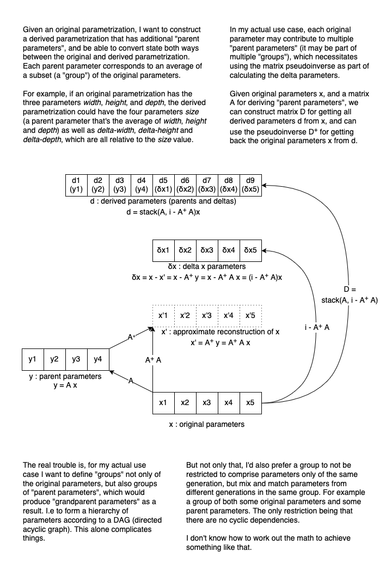
For my procedural creatures, I'm still working on a (generic mathematical) system for manually creating a derived higher-level parametrization based on an original parametrization.

I got some great pointers about using the matrix pseudoinverse and made a working implementation of that which works for one level of "parents", but I'm still unsure how to expand this approach to support an arbitrary hierarchy of parent parameters.

Diagram of how to manipulate parameters using matrices. Also some paragraphs of text: Given an original parametrization, I want to construct a derived parametrization that has additional "parent parameters", and be able to convert state both ways between the original and derived parametrization. Each parent parameter corresponds to an average of a subset (a "group") of the original parameters. For example, if an original parametrization has the three parameters width, height, and depth, the derived parametrization could have the four parameters size (a parent parameter that's the average of width, height and depth) as well as delta-width, delta-height and delta-depth, which are all relative to the size value. In my actual use case, each original parameter may contribute to multiple "parent parameters" (it may be part of multiple "groups"), which necessitates using the matrix pseudoinverse as part of calculating the delta parameters. Given original parameters x, and a matrix A for deriving "parent parameters", we can construct matrix D for getting all derived parameters d from x, and can use the pseudoinverse D+ for getting back the original parameters x from d. The real trouble is, for my actual use case I want to define "groups" not only of the original parameters, but also groups of "parent parameters", which would produce "grandparent parameters" as a result. I.e to form a hierarchy of parameters according to a DAG (directed acyclic graph). (...)
Quiet public
Rune Skovbo Johansen

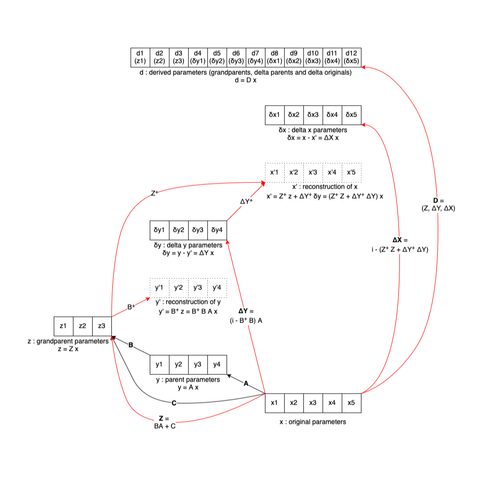
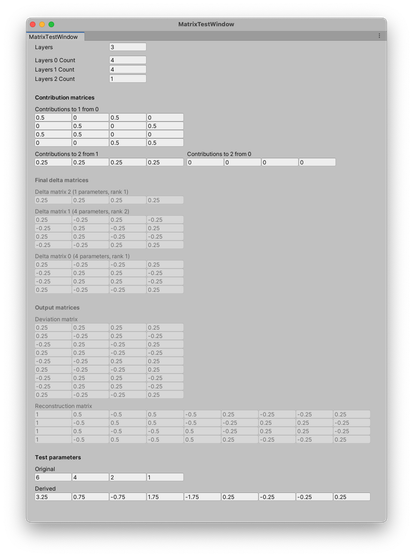
I managed to work out the generalized matrix logic for arbitrary layers of parents, where each parent can pick children from not only the layer immediately below, but any layers below. I have it fully working in a test window - now to integrate it into my parametrization framework...

Schematic showing the logic for three layers (originals X, parents Y and grandparents Z).
Screenshot of test window showing various input vectors and matrices and various calculated matrices based on the input.
Rune Skovbo Johansen

Turned out there was a flaw in the logic above. Groups mixing contributions from multiple different lower levels didn't work right. I went back to my earlier idea of stacking matrices before using the pseudoinverse on them. This worked.

Mar 23, 2025, 05:31 PM·Quiet public·Phanpy
0boosts·2favorites
Quiet public
Rune Skovbo Johansen

But then I noticed some patterns, and suspected I could simplify more. Instead of having different matrices with sizes corresponding to the parameters per layer, I could use large matrices corresponding to all the parameters at once. And I found out I could furthermore do the calculations for all layers at once too in one single swoop. The calculations I have in code now are much, much simpler than what I had before, and take up only a third as many lines.

Quiet public
Rune Skovbo Johansen

Here is the entirety of the calculations I've ended up with. It is *so simple* compared to all the complex diagrams and implementations for them I had earlier.

To summarize the goal, the idea is to construct matrices to convert from a source parametrization to a derived parametrization, and back. The derived parametrization is based on the source parameters (the base parameters) plus additional group parent parameters which are averages of multiple other parameters, including other group parent parameters. The order of a group parent is one higher than the highest ordered parameter in the group; base parameters have order 0. In the derived parametrization, parameters that are part of groups only store their delta compared to what can be approximated based on the group parent parameters. It’s similar to if grouped parameters stored their delta compared to the group average, except that approximations generalize the concept of average so it also works when parameters are part of multiple groups at once. All matrices are m × m, where m is the total number of derived parameters, including base parameters.
Input matrices base matrix: A 1 in the diagonal for each parameter that comes from the source parametrization. contribution matrix: For each group parent row, specify weights of contributing parameter columns. Calculation matrices conversion matrix: (base + contribution) ^ (highest_order - 2) approximation matrix: pseudoinverse(contribution) ⋅ contribution identity matrix: 1s along the diagonal. delta matrix: identity - approximation Output matrices derivation matrix: delta ⋅ conversion reconstruction matrix: pseudoinverse(derivation)
Quiet public
Tom Forsyth

@runevision Big sparse matrices make the world go round!

Quiet public
Rune Skovbo Johansen

@TomF Apparently! I still have basically no practical experience with (non graphics related) data matrices for anything else than what I've been working on here, but I've felt my intuition leveling up and repeatedly found matrix math lead to simple and beautiful satisfying solutions.

Quiet public
Tom Forsyth

@runevision They're simple and satisfying, but there's a massive number of 0.0f in those matrices, and often quite a few integers.

So sure - not many lines of code - but it can be considerable work for compilers and runtime libraries to remove those pointless multiplies.

Once you have a working solution, it's a very good idea to go back and figure out where all the zeros are and express the actual code in a more efficient way.

The poster-child for this is AI of course :-)

Quiet public
Rune Skovbo Johansen

@TomF I’m using C# library math.net which has a sparse matrix representation option. I’m not currently using it since I haven’t experienced any performance issues so far (and I assume it has trade offs), but I assume if need be it can address the issue better than I could myself.

Quiet public
Tom Forsyth

@runevision Well no. It you know that a value is never not-0, you can encode that yourself with a smaller matrix or a set of smaller submatrices. It takes effort for it to discover this stuff.

But yeah, at this stage you shouldn't worry about it. Finish the algo, then start tuning it.

Quiet public
Rune Skovbo Johansen

@TomF The heavy calculations happen at edit time. The result is a derivation matrix and a reconstruction matrix. Those don’t change at runtime and are only used for multiplication with vectors. So whatever values are or are not zero stay that way once calculated.

ExploreLive feeds
About