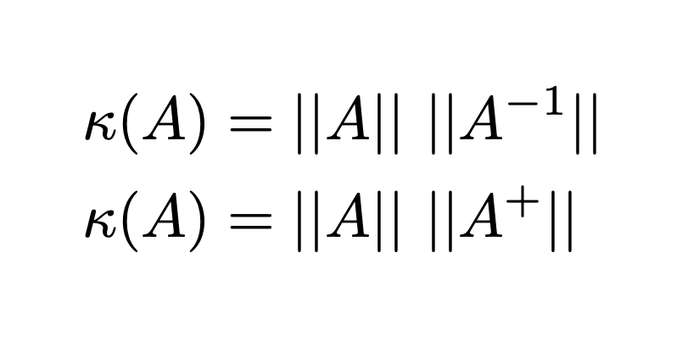Back

A nice aspect of the math behind this, which is not conveyed in the video, is that the more high-level parameters I create, the better the results also become when rolling random creatures by setting all parameters to random values.

There's more details on the concept and the math behind it in this post from a few days ago:
https://mastodon.gamedev.place/@runevision/114213218833400674

I had a scare today when after working more on the parametrization, the matrix numbers produced by the final pseudoinverse became very large, causing the creature meshes to "explode" and even Unity to crash. (1/2)

After digging a bit online, it seems that in the singular value decomposition used as part of the pseudoinverse, it's common to set singular values below a given threshold to zero to avoid instabilities. The Math.Net pseudoinverse implementation I use doesn't provide any control, but I reimplemented the method with threshold parameter. I had to set it super large (0.01) to avoid the issues, but then it seems to work. (2/2)

Here's a video showing what I'm talking about regarding instability of the pseudoinverse and how I'm working around it. But I'd like to understand better what's going on. #math

@kepeken The sums in the other direction is what the pseudoinverse calculates so to speak. It's not intuitive to author the values that way from the beginning.

I have learned about a concept called equilibration which might be useful, but it seems very niche with only academic sources about it that are a bit above my head.

@runevision Thanks for helping me understand better. I think you will not find a method to invert that matrix in those cases, because its singularity is telling you something valid and important.

If the group averages you have defined are accidentally overlapping in the information they provide, such that there is not enough information to determine all the parameters, that makes the matrix singular. That is not a problem with the algorithm, it is a sign that different/more groups are needed.

@runevision There might be some constraints that you want on the parameter values other than the group averages. If the pseudo-inverse is helping, it is helping because it implicitly applies those constraints, and furthermore they would be linear constraints.

If you can figure out what they are, it could improve the reliability if they were made explicit. The implicit constraints applied by the pseudoinverse are that certain sums are zero, that are dot products with the SVD columns with 0 S.V.

@lisyarus Does that refer to a specific calculation, or do you just mean the same way as I did for the pseudoinverse matrix? I didn't, but given all the numbers in the original matrix are small (between 0 and 1) and given how matrix-vector multiplication works, it should be very stable, similar to how the pseudoinverse is stable once it only has small numbers.

@runevision @lisyarus I think the condition number is analogously defined for the pseudo inverse matrix A^+, so very small values in A may result in very large values in A^+ I would think.

@shanecelis @lisyarus Ok, if I understand right. The L2 norm of the input matrix, pseudoinverse matrix and the multiplication of those two norms (the condition number) are by default 0.87, 1192.46, 1040.80. If I set the two small singular values to zero, then the numbers change to 0.87, 1.45, 1.27.